从零开始学统计 10 | 通俗易懂的 P 值
怎么计算P值
抛两次硬币,计算两次都为正(H)的概率
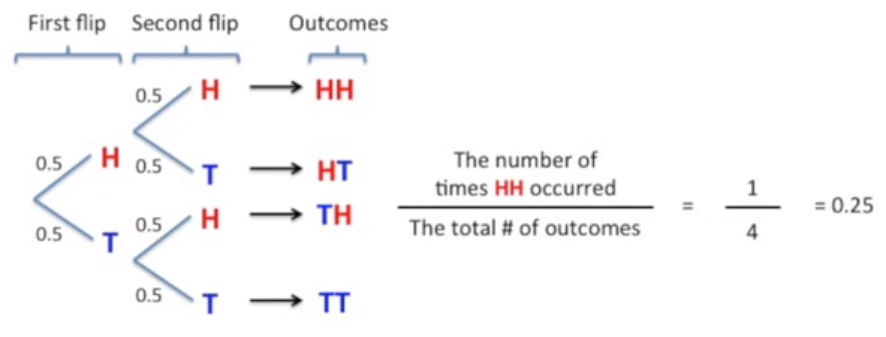
计算的P值由三个部分组成:
- 在观察到,在随机事件中发生的概率
- 与之概率相等的事件的概率
- 任何比观察的更罕见的事件发生概率
抛 5 次硬币,计算都为正(H)的概率,与P值
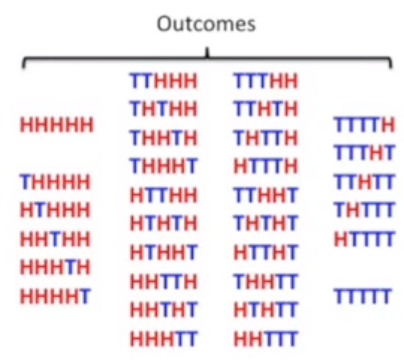
概率为
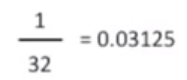
P值由三部分组成:
- 5个正面
- 5个反面
- 没有比这个事件更小的概率事件
所以计算得到
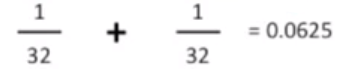
可以看到 p 值不小于 0.05(显著性阈值)
计算四个正面,一个反面的概率:
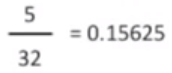
p 值由三部分组成
- 4正1反
- 1正4反
- 5正+5反
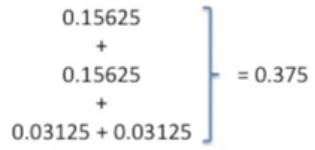
可以看到 p 值更不小于 0.05(显著性阈值),说明这个事件相对常见。
但是有个问题,如果是大样本量的话,不可能去列出所有的可能的
这时,就需要用到我们之前提到的分布
下图表示身高分布
曲线下面积表示一个人在范围内的身高概率
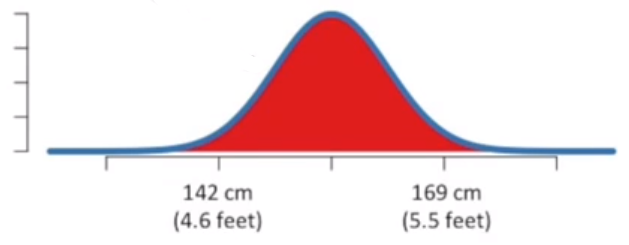
可以发现,曲线下 95 %的面积在身高 142 ~ 169cm,表示身高在这个范围内的概率。也就是说,测量一个人身高时,得到身高在 142 ~ 169cm 间的概率在 95%。
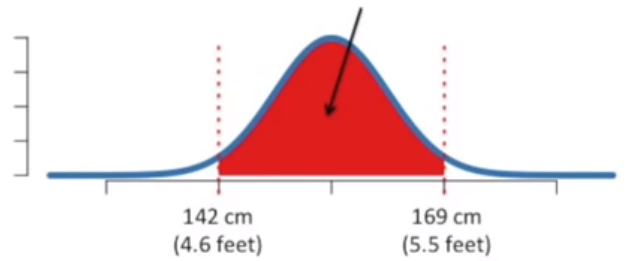
曲线下有 2.5 % 的总面积对于的高度大于 169cm。也就是说,测量一个人时,她身高大于 169 cm的概率是2.5%。
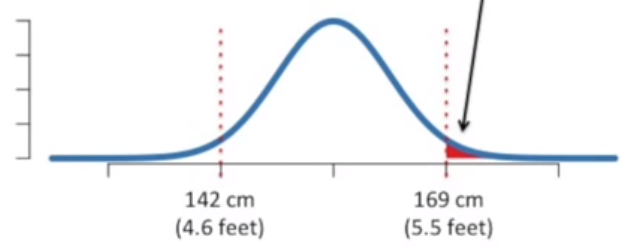
曲线下有 2.5 % 的总面积对于的高度小于 142cm。也就是说,测量一个人时,她身高小于 142 cm的概率是2.5%。
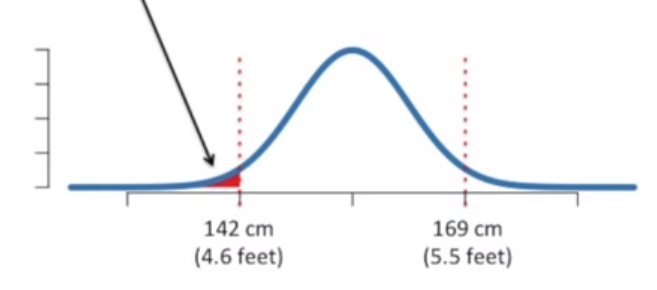
了解到这些,计算 p 值就很简单了,只需要将相应的面积百分比相加就行。
现在计算身高超过 169cm 的身高 p 值。回忆下 p 值由三部分构成:
- 在随机事件中发生的概率(>169cm):2.5%
- 与之概率相等的事件的概率(<142cm):2.5%
- 任何比观察的更罕见的事件发生概率:0
在图中标记出来:
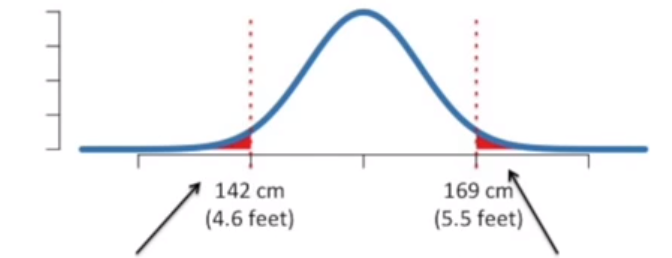
p 值 = 2.5% + 2.5% = 5% = 0.05
计算身高在 155.4cm ~ 156cm 间的人的p值是多少?
第一部分:这个身高区间,计算得到的面积是 4%
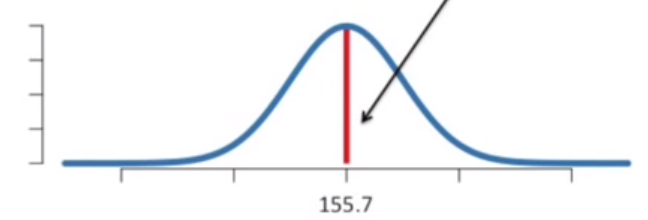
第二部分:< 155.4cm 的面积 48% 与 > 156cm 的面积为48%,二者相加为96%
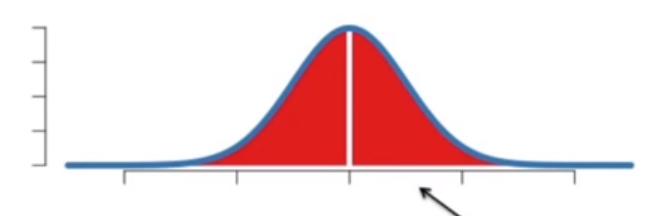
第三部分:无
p 值 = 4% + 96% = 1
虽然这个区间的概率很小只有4%,但是 p = 1,代表这段身高区间的人并没什么特别之处。
单尾与双尾的P值
现在发明了一种新的癌症治疗方法,我们要看用新治疗方法与旧治疗方法的效果比较。
对 6 个病人做治疗,新方法治疗(红点),旧方法治疗(黑点),在数轴上从左到右依次由好变坏。

单尾 P 值检验是新治疗优于旧治疗方法的假设。
双尾 P 值检验是新治疗是否更好,更差或没有显著差异。
单尾检验 P 值更小,意味着它不区分较差和无显著差异。
但是,现在我们想知道的是:新方法是否比旧治疗法更好还是更差。这时候最好使用双尾检验。
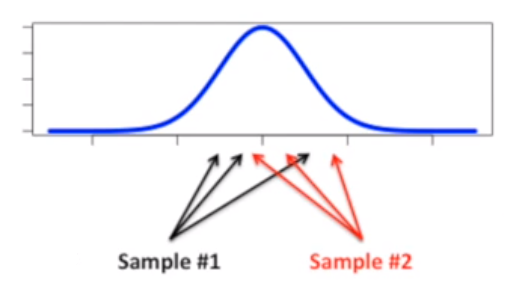
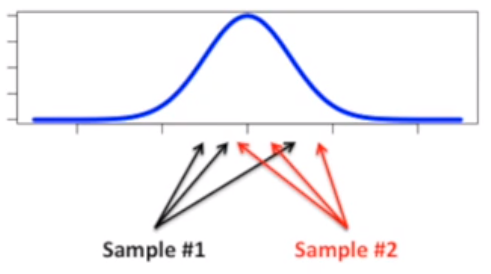
分别取两次样本,一次取三个数据
一种常见的情况像下图这样,两个样本会有重叠区域。这样得到的双尾t检验 P 值肯定是大于 0.05 的。
一种不常见的情况是,两个样本分的很开。双尾t检验会给一个小于0.05的 p 值。这种就是常说的假阳性,发生概率在 5 %。
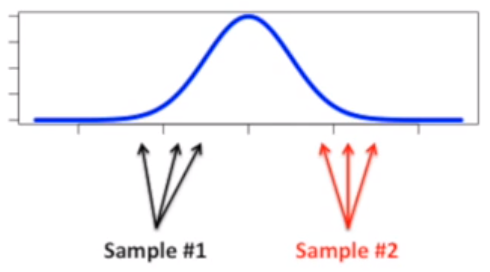
为什么是 5 %?
从正态分布的数据中,重复抽样 10000次
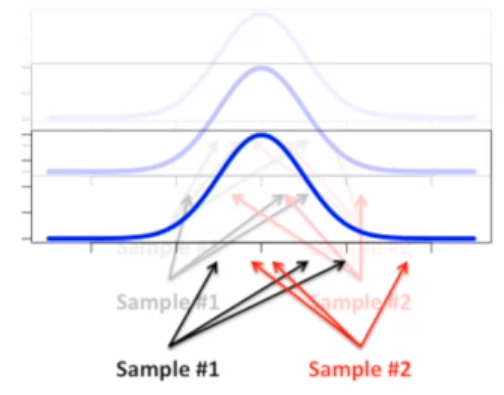
将每次抽样的 p 值计算下,作图
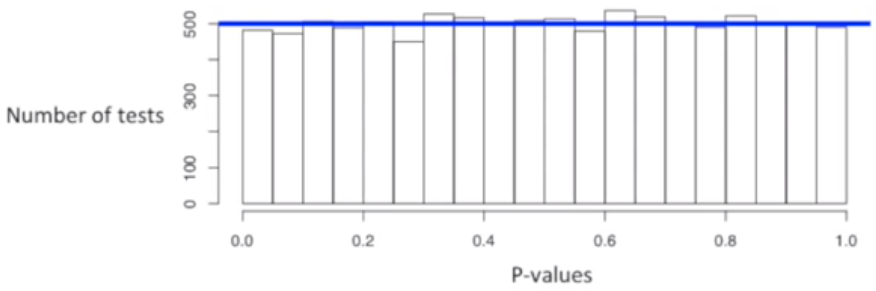
可以看到 p 值小于 0.05 的个数大约是 500,计算 p 值 500/10000 = 5%
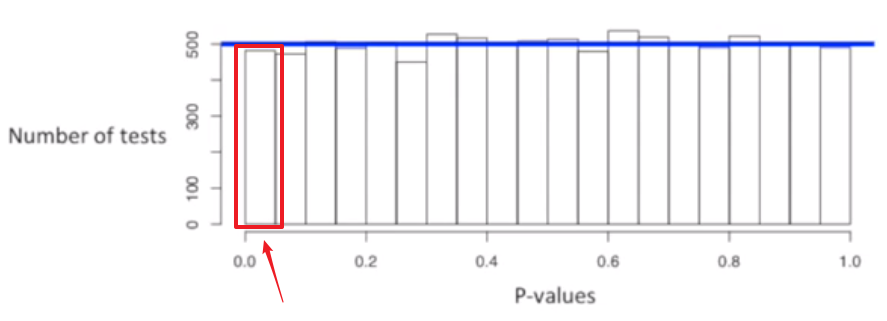
现在样本一中的两个以上的值小于样本二中所有的值,用单尾 t 检验
现在有 800 个假阳性,那么假阳性率为 8 %。但是刚刚我们还使用 0.05 来作为显著性阈值。
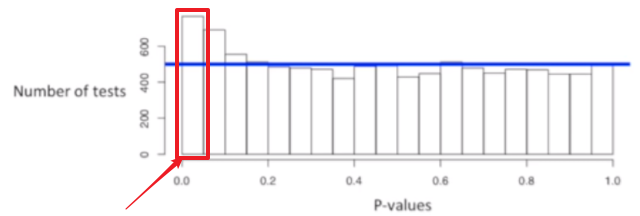
所以,不能看到数据后才决定使用单尾 p 值。
实际上,对于所有数据都有单尾或双尾 p 值,一般都要选择双尾的 p 值。
抽样分布
单一分布中抽样
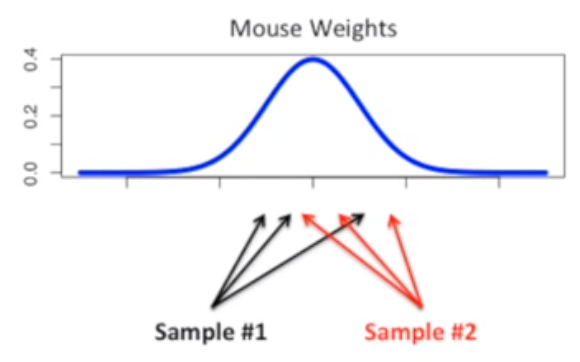
比如,现在从分布中抽取 2 组样本,每组 3 个样本。每个样本抽到的几率相等。
进行T检验,由于是同一分布,T检验会给我们一个很大的P值(表示两组样本很相关)。通过大量的检验,我们可以得到T检验给出大P值的概率。
两个独立分布中抽样
但是,这里假设要从两个独立分布中抽取样本:
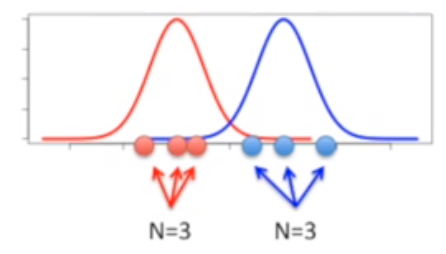
两个独立分布代表两组样本相关性很小,T检验就会给出很小的P值。
如果样本量大,我可以做多次T检验,查看T检验给出小P值的概率。
这个是为了检测是否需要增加样本量,排除是否因为抽样问题造成统计误差。
致谢:








