从水果连连看到两条序列比对
一、序列比对 Sequence Alignment
序列比对(sequence alignment),目前是生物信息学的基本研究方法。
算法类似于连连看,规则是上下两个水果一样,就可以连起来,计如得分:

现在如果上下两行代表两条序列,把水果换成碱基,可消除的碱基中间连线,就像下面这样:
|
到目前为止,我们已经实现了一个简单的序列比对。
序列比对最终结果可以用比对得分来评估,然后通过统计学分析后,得到序列间的相似性与同源性,以及它们的显著性水平即可进行下一步生物信息分析。
在应用上,如果找到了不同序列之间的相似性,那就可以推断功能或建立进化关系,以此更好地了解基因的起源和功能。
反之,如果找到序列间的不相似性,就能推断插入,突变,缺失等生物学过程,比如推断新冠病毒的突变位点。
根据序列比对范围和目的,分为两种:
1、全局比对 Global Alignment
顾名思义,就是对两条序列的全长都进行比对
|
当然有时候序列比对时会不尽人意,类似于这样:
|
细心的小伙伴可能会发现只有在其中空一格就会“连”到更多的碱基
|
其中引入的空格,也叫空位(Gap),在生物学中也有依据:DNA 序列在进化过程中会发生的碱基删除事件。但更多的是一种算法规则,即在计算打分时,需要遵循以下规则:
碱基匹配加分:+1,也就是中间有连线的碱基对
碱基错配罚分:-1,也就是没有连线的碱基对
碱基空位罚分:-3,也就是空位,不组成碱基对
根据规则,上述的比对结果为:8-1-3=4
这种比对常常用于基因家族分析,系统发育树构建等
2、局部比对 Local Alignment
目的是在两条序列比对后,获取序列比对分数或置信度最高的匹配序列片段。我们拿刚刚的全局比对结果举例
|
最佳的片段为
|
根据规则计算比对分数为:7,显然这就是我们要找的最佳匹配序列。
这种比对常常用于功能域查找,转录因子足迹搜索等等。
!!!
但是有个坏消息是,现实中的序列是要长的多,比如癌基因 p53 的序列长度为 25760 个碱基。
而且也要复杂的多,比如氨基酸之间的错配,由于氨基酸之间的物化性质,虽然是不同的氨基酸,但是介于错配与匹配分数之间,这就不能用简单的规则来计算比对分数啦。
为了获得最佳的比对序列,就需要比较序列间的比对得分大小。那么现在有两个需要解决的问题:
- 设计一种规则,用于计算最真实的比对得分
- 设计一种算法,来快速精准的比对序列
这时,有大牛提出计分矩阵和最优比对算法来解决这两个问题。
这篇我们先来探讨比对的得分的计算,也就是计分矩阵的由来与计算方法:
二、计分矩阵 Scoring Matrix
在序列比对过程中,需要一个计分规则来对匹配到的每个位置的碱基,氨基酸,错配等进行打分,因此该矩阵也叫替换矩阵(substitution matrix)。
2.1 碱基计分矩阵
比如我们来计算下面两条 DNA 序列的分值:
|
一个常用与DNA序列的计分矩阵
| A | T | C | G | |
|---|---|---|---|---|
| A | 0.9 | -0.1 | -0.1 | -0.1 |
| T | -0.1 | 0.9 | -0.1 | -0.1 |
| C | -0.1 | -0.1 | 0.9 | -0.1 |
| G | -0.1 | -0.1 | -0.1 | 0.9 |
这个矩阵的意思就是,只有匹配一样计分 0.9,但凡不一致扣分 0.1。根据这个计分规则,我们可以很骄傲地拿出我们幼儿园学到的数学,得出:
$0.9\times6 + 1\times(-0.1) = 5.3$
同源性:代表两条序列间有进化关系,也就是进化中的突变概率也会被考虑在内。
相似性:只代表两条序列的相似度
空位问题 Gap
对于序列在进化过程中,插入或缺失造成的序列空位,可能是一个或多个碱基,氨基酸,甚至功能域。
在进行序列比对时,就需要考虑到这些问题,一般用空位罚分(Gap penalty)来处理。
用公式表示:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EtIziru2-1635057569192)(https://cdn.nlark.com/yuque/__latex/525b352e7a54a951ffcc86e433a2f25b.svg)]
这里的参数代表:
a 空位设置 Gap opening:只要有一个空位出现,就以空位设置罚分
b 空位扩展 Gap extension:任一空位的扩大,以空位扩展罚分,一般长度越大,罚分越重
k 空位数
很容易可以得到
| 空位设置 | 空位扩展 | 用途 |
|---|---|---|
| 大 | 大 | 用于非常相似的蛋白质序列的比对,也就是序列间极少有插入,缺失 |
| 大 | 小 | 用于功能域插入或缺失的蛋白质序列比对,序列间少量的长片段空缺 |
| 小 | 大 | 用于亲缘关系较远的蛋白质同源性分析,序列间有大量的短片段空缺 |
2.2 氨基酸计分矩阵
蛋白质序列的计分矩阵相较于只有 4 个碱基的 DNA 序列要复杂的多。对于蛋白质序列的分析可以避免在翻译时的简并性问题(几个三联体可能编码同一个氨基酸),而且也是最接近执行生物学功能和自然选择的分子,因此蛋白质分析在同源家族,基因进化等方面更具研究意义。
2.2.1 PAM 矩阵
各种氨基酸在进化过程中,由于其自身的物化性质,一种氨基酸替换为另一种氨基酸的概率并不一样。

1978年,以 Dayhoff 为首的科学家,对大量蛋白质家族进行统计学分析,观测到 1572 次氨基酸替换,构建了最原始的 PAM 矩阵(Percent Accepted Mutation,PAM),也叫 MDM 矩阵(Mutation Data Matrix)或 Dayhoff 矩阵。
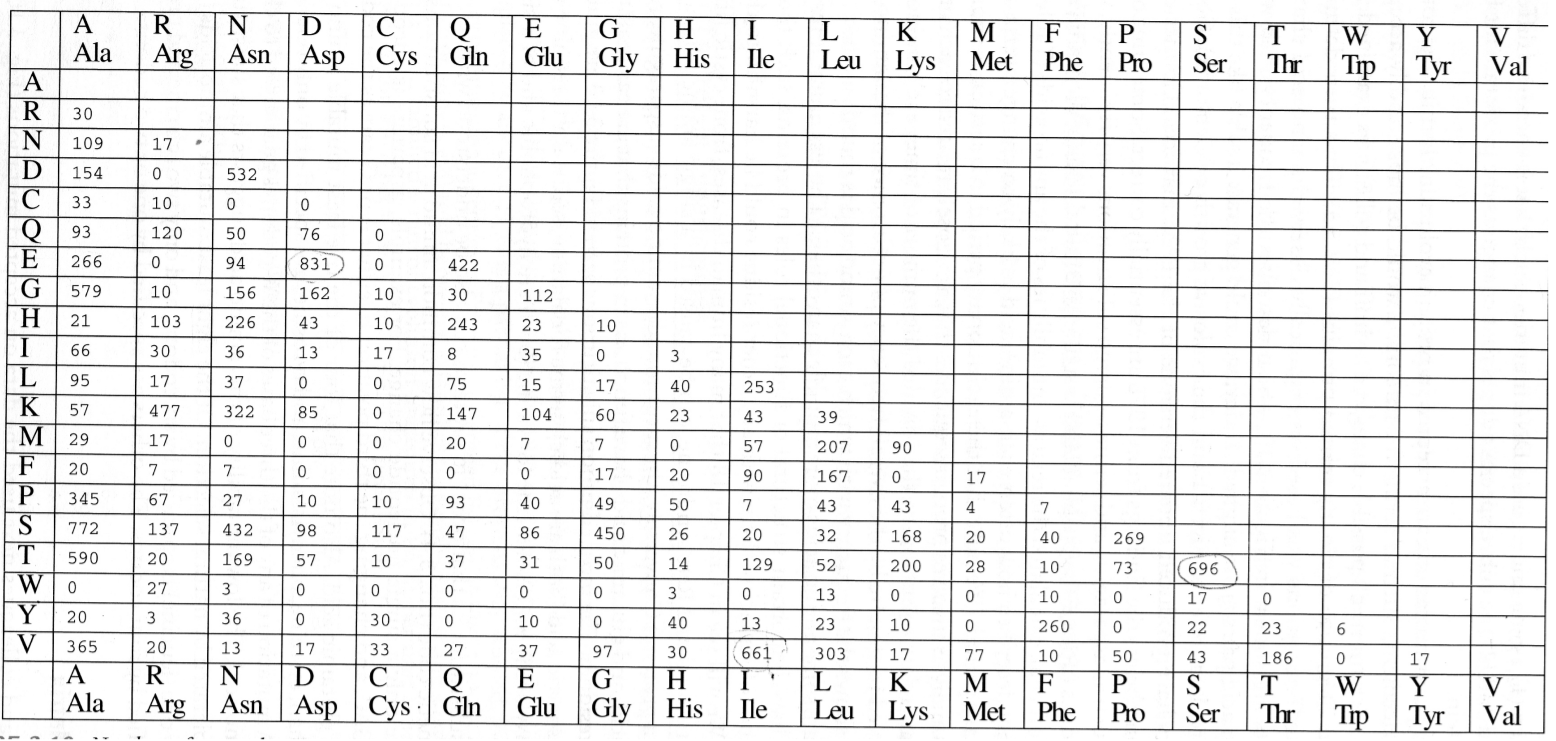
根据该表可以计算突变概率矩阵,其中每个矩阵元素代表在进化过程中氨基酸之间的替换频率。
接下来将观测到的突变百分率作为一种进化时间单位,现在假设同一位点不会发生两次以上的突变,我们对 PAM 进行次方处理,比如 PAM 的 100 次方,意味着进化了 100 次,时间尺度也会更大。
在Dayhoff 和她的小伙伴研究过程中,发现将突变概率矩阵进行 250 次方处理后得到的 PAM 250,适合用于研究远缘蛋白质进化,换句话说这是一个研究这种蛋白质最合适的时间尺度。
然后再将 PAM 250 矩阵进行对数处理,得到 PAM250 的对数概率矩阵,该矩阵用于表示氨基酸间互相替换的观测规律。
经过前人的不懈努力,我们终于拿到了最终的计分矩阵,可以计算比对得分啦。
后来随着蛋白质序列的增加,有人扩大了统计样本,新构建了 JTT 矩阵等,但最终效果都与 PAM 类似。因此,目前使用最为广泛的还是 PAM。
不清楚选择哪种矩阵怎么办?
需要注意,由于不同的蛋白质家族进化速度并不相同,因此选用的 PAM 也会不一样。
总的来说,如果研究进化关系远的蛋白质序列,最好选 > 100 PAM。
如果蛋白质序列本身相似度高,PAM 的影响会比较小,默认 PAM250 就行。
2.2.2 BLOSUM 矩阵

1992 年,Steve Henikoff 和他的妻子 Jorja Henikoff 一起引入了 BLOSUM 替换矩阵。
BLOSUM(Blocks Substitution Matrix),不同于 PAM 直接用全序列对统计氨基酸替换规律,Henikoff 先对区域保守的蛋白质家族进行局部对比,得到蛋白质序列的高度保守区域,也就是 Blocks,然后基于局部比对块获得每个位置的替换分数。
在计算时首先要构建一个蛋白质家族最保守区域的序列比对数据库,得到局部比对块,计算块中的氨基酸对。
现在计算每个氨基酸对的替换分数:
a. 计算观察概率
假设 $f_{ij}$ 代表 i,j 氨基酸对,$q_{ij}$ 代表观察到的氨基酸频率:
$q_{ij}=\frac{f_{ij}}{\sum{f_{ij}}}$
b. 计算期望概率
在完全独立情况下,$p_i, p_j$ 代表 i,j 氨基酸频率,该氨基酸替换频率的期望值 $e_{ij}$
$e_{ij}=\begin{cases}
p_i^2 & i=j \
2p_ip_j & i≠j \
\end{cases}$
其中,
$p_i=q_{ii}+\frac{1}{2}\sum_{i≠j}{q_{ij}}$
c. 计算氨基酸替换分数
$score_{ij}=2log2(\frac{q_{ij}}{e_{ij}})$
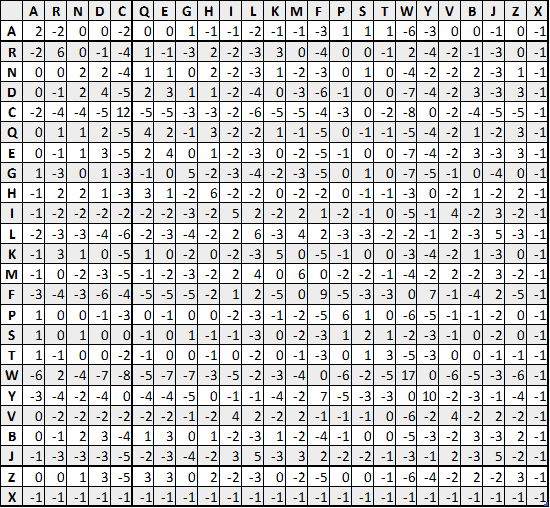
也就是,$q_{ij}$ 代表观察到的可能性,$e_{ij}$ 代表预料之中的可能性。每个氨基酸对的出现与该对出现的预期值的比率,再被四舍五入并用于替换矩阵中,得到这样一种矩阵,类似于 PAM 矩阵:

其中,
零分表示在数据库中发现给定的两个氨基酸比对的频率是偶然的
正分表示比对被发现的频率高于偶然
负分表示比对被发现的频率低于偶然
根据构建数据库时, Block 的最小相似比例,可以定义不同的 BLOSUM。
比如上图所示的是 BLOSUM 62, 代表使用局部序列比对相似度为至少为 62%的 Block 构建的替换矩阵。
不难理解,BOLSUM 后的数字越大,代表进化关系越近。
不清楚选择哪种矩阵怎么办?
BLOSUM 80:进化关系近的蛋白质
BLOSUM 62:大部分蛋白质,默认
BLOSUM 45:进化关系远的蛋白质
目前 BLOSUM 矩阵就是我们使用 BLAST 算法经常用的一种计分矩阵。
2.2.3 PSSM 位置特异性矩阵
位置特异性矩阵(PSSM,Position-Specific Scoring Matrix),计算每种碱基或氨基酸,在特定位置的频率矩阵。一般常用于保守序列的搜索,比如PSI-BLAST,DELTA-BLAST等。
计算举例:
|
a. 计算频数矩阵
对每条序列中的 ATCG 计算频数
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 总 | |
|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 0 | 2 | 0 | 0 | 0 | 4 | 1 | 7 |
| T | 4 | 0 | 0 | 0 | 2 | 0 | 0 | 3 | 9 |
| C | 0 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 3 |
| G | 0 | 3 | 2 | 4 | 0 | 4 | 0 | 0 | 13 |
b. 计算频率矩阵
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 总 | |
|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 0 | 0.5 | 0 | 0 | 0 | 1 | 0.25 | 0.22 |
| T | 1 | 0 | 0 | 0 | 0.5 | 0 | 0 | 0.75 | 0.28 |
| C | 0 | 0.25 | 0 | 0 | 0.5 | 0 | 0 | 0 | 0.09 |
| G | 0 | 0.75 | 0.5 | 1 | 0 | 1 | 0 | 0 | 0.41 |
c. 标准化矩阵
碱基背景频率/位置频率
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 总 | |
|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 0 | 2.27 | 0 | 0 | 0 | 4.55 | 1.14 | 0.22 |
| T | 3.57 | 0 | 0 | 0 | 1.79 | 0 | 0 | 2.68 | 0.28 |
| C | 0 | 2.78 | 0 | 0 | 5.56 | 0 | 0 | 0 | 0.09 |
| G | 0 | 1.83 | 1.22 | 2.44 | 0 | 2.44 | 0 | 0 | 0.41 |
d. 对数转换矩阵
$score=log_2(p_{ij})$,其中 $p_{ij}$ 代表标准化矩阵中对应的频率,如果 $p_{ij}$ 为 0,则取 $p_{ij}$ 伪值 0.1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| A | -3.3 | -3.3 | 1.18 | -3.3 | -3.3 | -3.3 | 2.19 | 0.19 |
| T | 1.84 | -3.3 | -3.3 | -3.3 | 0.84 | -3.3 | -3.3 | 1.42 |
| C | -3.3 | 1.48 | -3.3 | -3.3 | 2.48 | -3.3 | -3.3 | -3.3 |
| G | -3.3 | 0.87 | 0.29 | 1.29 | -3.3 | 1.29 | -3.3 | -3.3 |
实际应用中,可以用该 PSSM 矩阵作为打分矩阵,去搜索未知序列中与该 PSSM 相似的保守序列片段。当然也可以计算并绘制基序 Logo。
下一篇我们详细探究序列比对算法:
- Needleman-Wunsch 算法
- Smith-Waterman 算法







