从零开始学统计 11 | 理解置信区间
置信区间
假设现在测量了12个小鼠体重的值,注意这里只测量了12只小鼠(样本),而不是地球上的每一只小鼠(总体)
取12个测量值,计算平均值,注意这里是样本均值,而不是总体均值(地球上所有小鼠的均值)
理解样本均值与总体均值:https://zhenglei.blog.csdn.net/article/details/108392410
但是,我们可以通过 Bootstrap 方法,确定一个比较合理的均值范围来代表小鼠总体均值
随机选12个小鼠体重值
Boostrap 是可放回抽样,意味着抽样时可能会抽到同一个值
计算随机样本的均值

重复1,2步,重复次数大于10000

现在,选择95%的bootstrap过程中产生的均值,下面画一条黑线,这段范围就是置信区间

因为这个置信区间可以覆盖 95% 的平均值,除此之外发生的概率只有 5%。换句话说,在置信区间外的P值都小于 0.05,意味着有统计显著差异。
我们开始的计算的样本均值,是对所有小鼠总体均值的估计,现在利用置信区间,我们就能知道小鼠总体均值和P值。
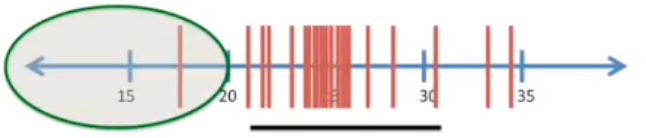
绿圈显示,测量均值落在该区域的概率小于 0.05,P值小于 0.05,说明这几乎不可能发生。
因此,根据置信区间,我们可以确定总体均值和任意小于20的数值之间在统计上都存在显著差异。
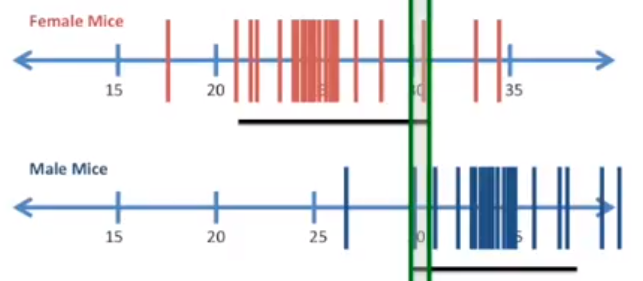
如果两个样本的置信区间有重叠,最好进行统计检验,如 t-test 来查看差异是否显著。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 白墨!
评论







